Cara Konversi Bilangan Desimal, Biner, Oktal & Heksadesimal
Konversi bilangan biasanya menjadi pengetahuan dasar yang sering atau mungkin wajib diberikan kepada mahasiswa pada mata kuliah pengenalan komputer. Karena pentingnya konsep dasar sistem bilangan dengan basis yang berbeda sehingga juga diajarkan atau diperkenalkan kepada siswa SMK/SMA atau bahkan siswa SMP. Ada empat basis bilangan yang sering dipakai yakni :
Berikut ini akan dibahas satu persatu bilangan tersebut serta bagaimana cara melaksanakan konversi antar basis bilangan :
Setiap digit dalam sebuah bilangan dalam basis 10 sanggup mempunyai besaran tertentu dalam basis 10.
Contoh:
1075 akan terdiri dari 1 ribuan, 0 ratusan, 7 puluhan dan 5 satuan, atau secara matematis sanggup ditulis sebagai :
1075 = (1x103) + (0x102) + (7x101) + (5x100)
Rumus Konversi Desimal ke Basis Bilangan Lainnya
Untuk melaksanakan konversi dari bilangan desimal ke basis bilangan lainnya, misal basis n, ialah dengan membagi bilangan tersebut dengan n secara berulang hingga bilangan bundar hasil bagi nya sama dengan nol. Lalu sisa hasil bagi dari setiap iterasi ditulis dari terakhir (bawah) hingga ke awal (atas). Untuk lebih jelasnya lihat pola konversi desimal ke basis lainnya pada klarifikasi berikutnya.

Konversi Desimal ke Biner
Dengan memakai rumus perhitungan konversi bilangan desimal ke basis lainnya kita sanggup lakukan sebagai berikut.
Contoh :
6710 = …….2 ?
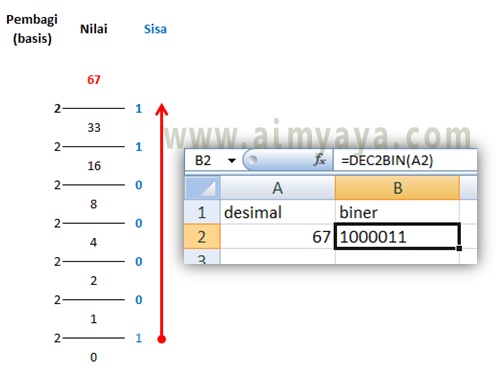
Misalkan kita akan melaksanakan konversi 67 basis sepuluh (desimal) ke dalam basis 2 (biner).
Konversi Desimal ke Oktal
Dengan rumus yang sama menyerupai biner kita sanggup lakukan juga untuk bilangan berbasis 8 (oktal).
Contoh:
6710 = …….8 ?
Konversi Desimal ke Heksadesimal
Seperti halnya biner dan oktal, kita pun akan memakai teknik perhitungan yang sama.
Contoh 1:
6710 = …….16 ?
Contoh 2:
9210 = …….16 ?

Konversi Biner ke Desimal
Untuk melaksanakan konversi dari bilangan biner atau bilangan berbasis selain 10 ke bilangan berbasis 10 (desimal) maka anda tinggal mengalikan setiap digit dari bilangan tersebut dengan pangkat 0, 1, 2, …, dst, dari basis mulai dari yang paling kanan.
Contoh :
101102 = …….10 ?
101102 = + 1x24 + 0x23 + 1x22 + 1x21 + 0x20 = 16 + 0 + 4 + 2 + 0 = 2210
Gunakan fungsi BIN2DEC() di microsoft excel untuk konversi biner ke desimal.
Konversi Biner ke oktal
Untuk melaksanakan konversi biner ke oktal lakukan bagi setiap 3 digit menjadi sebuah angka oktal dimulai dari paling kanan.
Contoh :
101102 = …….8 ?
Konversi Biner ke Hexadesimal
Konversi biner ke heksa desimal menyerupai dengan konversi biner ke oktal. Hanya saja pembagian kelompok terdiri dari 4 digit biner. Selain itu untuk nilai 10, 11, 12, .., 15 diganti dengan abjad A, B, C, …, F.
Contoh :
1110102 = …….16 ?

Konversi Bilangan Oktal ke Desimal
Untuk konversi oktal ke binner anda perlu mengalikan digit dengan pangkat dari bilangan 8.
Contoh :
3658 = …….10 ?
Untuk melaksanakan konversi bilangan oktal ke bilangan berbasis 10 (desimal) lakukan dengan mengalikan setiap digit dari bilangan tersebut dengan pangkat 0, 1, 2, …, dst, dari basis mulai dari yang paling kanan.
3658 = (3 x 82)10 + (6 x 81)10 + (5 x 80)10 = 192 + 48 + 5 = 245
Untuk fungsi konversi oktal ke decimal di ms excel gunakan OCT2DEC()
Konversi Bilangan Oktal ke Biner
Cara ini merupakan kebalikan cara konversi biner ke oktal. Setiap digit oktal akan eksklusif dikonversi ke biner kemudian risikonya digabungkan.
Contoh:
548 = …….2 ?
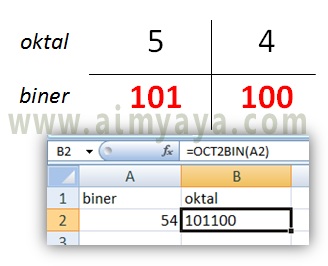
Konversi Bilangan Oktal ke Heksa desimal
Untuk perhitungan secara manual, konversi bilangan oktal ke desimal dilakukan dengan mengkonversi bilangan oktal ke bilangan basis antara terlebih dahulu. Ada dua cara yang sering dipakai untuk konversi oktal ke hexadecimal. Cara pertama konversi dahulu bilangan oktal ke desimal, kemudian dari bilangan desimal tersebut dikonversi lagi ke heksadesimal. Cara kedua ialah dengan menkonversi bilangan oktal ke bilangan biner, kemudian dari biner di konversi lagi menjadi bilangan heksadesimal. Cara kedua merupakan cara yang paling sering digunakan.
Contoh :
3658 = …….16

Konversi Bilangan Heksa desimal ke desimal
Untuk konversi heksadesimal ke desimal lakukan dengan mengalikan digit bilangan heksa dengan pangkat bilangan 16 dari kanan ke kiri mulai dengan pangkat 0, 1, 2, …, dst
Contoh :
F516 = …….8 ?
F516 = (15 x 161)10 + (5 x 16-0)10 = 240 + 5 = 245
Untuk fungsi konversi heksadesimal ke desimal di ms excel gunakan fungsi HEX2DEC()
Konversi Bilangan Heksadesimal ke Biner
Cara ini merupakan kebalikan cara konversi biner ke heksadesimal. Setiap digit heksadesimal eksklusif dikonversi ke biner kemudian risikonya dipadukan.
Contoh:
F516 = …….2 ?

Konversi Bilangan Heksa Desimal ke Oktal
Untuk konversi heksa desimal ke oktal menyerupai dengan cara konversi oktal ke desimal. Lakukan konversi heksadesimal ke biner terlebih dahulu kemudian dari binner di konversi lagi ke oktal.
Contoh :
F516 = …….8

Tips Cara Konversi Bilangan Desimal, Biner, Octal, dan Heksadesimal
Untuk perhitungan konversi bilangan secara manual memerlukan ketelitian, ketekunan dan latihan yang tekun. Untuk mengecek/menguji hasil perhitungan manual dari latihan yang anda lakukan gunakan fungsi konversi di microsoft excel yang telah disediakan.
- bilangan berbasis dua atau yang sering disebut dengan bilangan biner (binary), digit yang dipakai ialah 0 dan 1
- bilangan berbasis delapan atau sering juga disebut oktal (octal), digit yang dipakai ialah 0, 1, 2, …, 7
- bilangan berbasis sepuluh atau desimal yang sering kita dipakai dalam kehidupan sehari-hari, digit yang dipakai ialah 0, 1, 2, …, 8, 9; serta
- bilangan berbasis enambelas atau heksadesimal (hexadecimal), dengan digit yang dipakai ialah 0, 1, 2, 3, …, 8, 9, A, B, …, E, F. Dimana A sebagai pengganti nilai 10, B=11, C=12, dst.
Berikut ini akan dibahas satu persatu bilangan tersebut serta bagaimana cara melaksanakan konversi antar basis bilangan :
1. Bilangan Desimal
Bilangan desimal (decimal) merupakan bilangan dengan basis 10. Angka untuk bilangan desimal ialah 0, 1, 2, … , 8, 9. Bilangan ini sering kita gunakan dalam kehidupan sehari-hari.Setiap digit dalam sebuah bilangan dalam basis 10 sanggup mempunyai besaran tertentu dalam basis 10.
Contoh:
1075 akan terdiri dari 1 ribuan, 0 ratusan, 7 puluhan dan 5 satuan, atau secara matematis sanggup ditulis sebagai :
1075 = (1x103) + (0x102) + (7x101) + (5x100)
Rumus Konversi Desimal ke Basis Bilangan Lainnya
Untuk melaksanakan konversi dari bilangan desimal ke basis bilangan lainnya, misal basis n, ialah dengan membagi bilangan tersebut dengan n secara berulang hingga bilangan bundar hasil bagi nya sama dengan nol. Lalu sisa hasil bagi dari setiap iterasi ditulis dari terakhir (bawah) hingga ke awal (atas). Untuk lebih jelasnya lihat pola konversi desimal ke basis lainnya pada klarifikasi berikutnya.

Konversi Desimal ke Biner
Dengan memakai rumus perhitungan konversi bilangan desimal ke basis lainnya kita sanggup lakukan sebagai berikut.
Contoh :
6710 = …….2 ?
Misalkan kita akan melaksanakan konversi 67 basis sepuluh (desimal) ke dalam basis 2 (biner).
- Pertama-tama kita bagi 67 dengan 2, didapat bilangan bundar hasil bagi ialah 33 dengan sisa hasil bagi ialah 1, atau dengan kata lain 67 = 2*33 + 1
- Selanjutnya bilangan bundar hasil bagi tersebut (33) kita bagi dengan 2 lagi, 33/2 = 16, sisa hasil bagi 1.
- Kemudian kita ulangi lagi, 16/2 = 8, sisa hasil bagi 0.
- Ulangi lagi langkah tersebut hingga bilangan bundar hasil bagi sama dengan 0. Setelah itu tulis sisa hasil bagi mulai dari bawah ke atas.
- Dengan demikian kita akan mendapat bahwa 6710 = 10000112.
- Bila komputer/laptop anda tersedia microsoft excel, maka anda sanggup memakai fungsi DEC2BIN() untuk melaksanakan konversi dari bilangan desimal ke biner.

Konversi Desimal ke Oktal
Dengan rumus yang sama menyerupai biner kita sanggup lakukan juga untuk bilangan berbasis 8 (oktal).
Contoh:
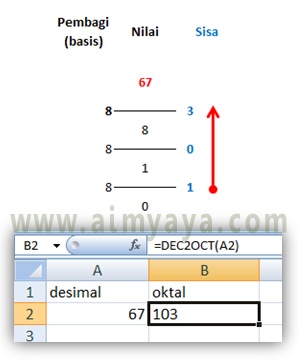
6710 = …….8 ?
- Pertama-tama 67/8 = 8, sisa 3
- Lalu 8/8 = 1, sisa 0,
- Terakhir 1/8=0, sisa 1.
- Dengan demikian dari hasil perhitungan didaptkan 6710 = 1038
- Anda juga sanggup memakai fungsi microsoft excel DEC2OCT() untuk konversi bilangan desimal ke oktal.

Konversi Desimal ke Heksadesimal
Seperti halnya biner dan oktal, kita pun akan memakai teknik perhitungan yang sama.
Contoh 1:
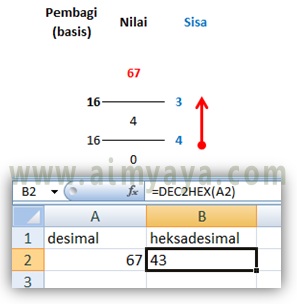
6710 = …….16 ?
- Pertama-tama 67/16 = 4, sisa 3
- Lalu 4/16 = 0, sisa 4,
- Dengan demikian dari hasil perhitungan didapatkan 6710 = 4316

Contoh 2:
9210 = …….16 ?
- Pertama-tama 92/16 = 5, sisa 12 (ditulis C)
- Lalu 5/16 = 0, sisa 5,
- Dengan demikian dari hasil perhitungan didapatkan 9210 = 5C16

2. Bilangan Biner
Bilangan biner (binary) merupakan bilangan berbasis dua. Angka dari bilangan biner hanya berupa angka 0 dan 1.Konversi Biner ke Desimal
Untuk melaksanakan konversi dari bilangan biner atau bilangan berbasis selain 10 ke bilangan berbasis 10 (desimal) maka anda tinggal mengalikan setiap digit dari bilangan tersebut dengan pangkat 0, 1, 2, …, dst, dari basis mulai dari yang paling kanan.
Contoh :
101102 = …….10 ?
101102 = + 1x24 + 0x23 + 1x22 + 1x21 + 0x20 = 16 + 0 + 4 + 2 + 0 = 2210
Gunakan fungsi BIN2DEC() di microsoft excel untuk konversi biner ke desimal.
Konversi Biner ke oktal
Untuk melaksanakan konversi biner ke oktal lakukan bagi setiap 3 digit menjadi sebuah angka oktal dimulai dari paling kanan.
Contoh :
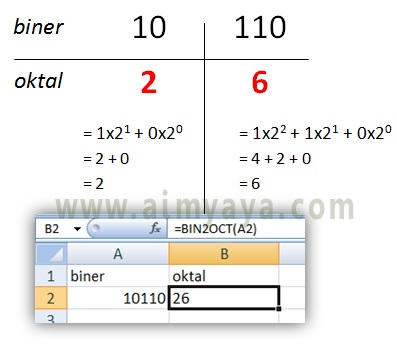
101102 = …….8 ?
- Pertama-tama bagi menjadi kelompok yang terdiri dari 3 digit biner: 10 dan 110.
- Kemudian konversi setiap kelompok dengan memakai perhitungan konversi biner ke desimal.
- Sehingga didapat 101102 = 268
- Anda juga sanggup memakai fungsi BIN2OCT yang disediakan di microsoft excel

Konversi Biner ke Hexadesimal
Konversi biner ke heksa desimal menyerupai dengan konversi biner ke oktal. Hanya saja pembagian kelompok terdiri dari 4 digit biner. Selain itu untuk nilai 10, 11, 12, .., 15 diganti dengan abjad A, B, C, …, F.
Contoh :
1110102 = …….16 ?
- Pertama-tama bagi menjadi kelompok yang terdiri dari 4 digit biner: 11 dan 1010.
- Kemudian konversi setiap kelompok dengan memakai perhitungan konversi biner ke desimal.
- Sehingga didapat 1110102= 3A16
- Anda juga sanggup memakai fungsi BIN2HEX() yang disediakan di microsoft excel

3. Bilangan Oktal
Bilangan oktal (octal) ialah bilangan berbasis 8. Sehingga angka digit yang dipakai ialah 0, 1, 2, …, 7, 8.Konversi Bilangan Oktal ke Desimal
Untuk konversi oktal ke binner anda perlu mengalikan digit dengan pangkat dari bilangan 8.
Contoh :
3658 = …….10 ?
Untuk melaksanakan konversi bilangan oktal ke bilangan berbasis 10 (desimal) lakukan dengan mengalikan setiap digit dari bilangan tersebut dengan pangkat 0, 1, 2, …, dst, dari basis mulai dari yang paling kanan.
3658 = (3 x 82)10 + (6 x 81)10 + (5 x 80)10 = 192 + 48 + 5 = 245
Untuk fungsi konversi oktal ke decimal di ms excel gunakan OCT2DEC()
Konversi Bilangan Oktal ke Biner
Cara ini merupakan kebalikan cara konversi biner ke oktal. Setiap digit oktal akan eksklusif dikonversi ke biner kemudian risikonya digabungkan.
Contoh:
548 = …….2 ?
- Pertama-tama hitung 58 = 1012 (Lihat cara konversi dari desimal ke biner)
- Lalu hitung 48 = 1002
- Sehingga didapat 548 = 1011002
- Anda juga sanggup memakai rumus di ms excel OCT2BIN() yang akan menkonversi bilangan oktal ke biner

Konversi Bilangan Oktal ke Heksa desimal
Untuk perhitungan secara manual, konversi bilangan oktal ke desimal dilakukan dengan mengkonversi bilangan oktal ke bilangan basis antara terlebih dahulu. Ada dua cara yang sering dipakai untuk konversi oktal ke hexadecimal. Cara pertama konversi dahulu bilangan oktal ke desimal, kemudian dari bilangan desimal tersebut dikonversi lagi ke heksadesimal. Cara kedua ialah dengan menkonversi bilangan oktal ke bilangan biner, kemudian dari biner di konversi lagi menjadi bilangan heksadesimal. Cara kedua merupakan cara yang paling sering digunakan.
Contoh :
3658 = …….16
- Konversi bilangan oktal menjadi bilangan biner
3658 = 11 110 101 2
angka 3, 6, dan 5 dikonversi terlebih dahulu menjadi biner. - Kemudian bilangan biner tersebut dikelompokkan setiap 4 digit dimulai dari yang paling kanan
- Selanjutnya 4 digit biner transformasikan menjadi heksadesimal
11 110 101 2 = F516

4. Bilangan Heksadesimal
Bilangan heksadesimal (hexadecimal)merupakan bilangan berbasis 16. Sehingga angka digit yang dipakai ialah 0, 1, 2, …, 8, 9, A, B, …, E, F dimana A s/d F merupakan nilai untuk 10 s/d 15 desimal.Konversi Bilangan Heksa desimal ke desimal
Untuk konversi heksadesimal ke desimal lakukan dengan mengalikan digit bilangan heksa dengan pangkat bilangan 16 dari kanan ke kiri mulai dengan pangkat 0, 1, 2, …, dst
Contoh :
F516 = …….8 ?
F516 = (15 x 161)10 + (5 x 16-0)10 = 240 + 5 = 245
Untuk fungsi konversi heksadesimal ke desimal di ms excel gunakan fungsi HEX2DEC()
Konversi Bilangan Heksadesimal ke Biner
Cara ini merupakan kebalikan cara konversi biner ke heksadesimal. Setiap digit heksadesimal eksklusif dikonversi ke biner kemudian risikonya dipadukan.
Contoh:
F516 = …….2 ?
- Pertama-tama hitung F16 = 11112 (F16 = 1510 = 11112, Lihat cara konversi dari desimal ke biner)
- Lalu hitung 516 = 01012 (harus selalu dalam 4 digit biner, kalau nilai hasil konversi tidak mencapai 4 digit biner maka tambahkan angka 0 di depan hingga menjadi 4 digit biner)
- Kemudian didapat F516 = 111101012
- Fungsi di ms excel yang sanggup anda gunakan untuk mengkonversi heksadesimal ke biner ialah HEX2BIN()

Konversi Bilangan Heksa Desimal ke Oktal
Untuk konversi heksa desimal ke oktal menyerupai dengan cara konversi oktal ke desimal. Lakukan konversi heksadesimal ke biner terlebih dahulu kemudian dari binner di konversi lagi ke oktal.
Contoh :
F516 = …….8
- Konversi bilangan heksadesimal menjadi bilangan biner
F516 = 1111 01012
angka F dan 5 dikonversi terlebih dahulu menjadi biner. - Kemudian bilangan biner tersebut dikelompokkan setiap 3 digit dimulai dari yang paling kanan
- Selanjutnya 3 digit biner transformasikan menjadi oktal
11 110 101 2 = 3658

0 Response to "Cara Konversi Bilangan Desimal, Biner, Oktal & Heksadesimal"
Posting Komentar